C’est un fait expérimental la vitesse de la lumière est constante. Que l’on soit immobile ou en mouvement, quelle qu’en soit la direction, la mesure de la vitesse de la lumière donne toujours le même résultat. Dans le vide, elle est de 299 792 458 mètre/seconde.
Ceci a été démontré, entre autres, par l’expérience de Michelson et Morley. Cette constance a un impact considérable sur les mesures des phénomènes physiques et ce qui en découle.
En partant de ce constat, analysons une expérience qui met en jeu un faisceau lumineux. Voyons les conclusions que nous pourrons en tirées.

Un chariot est immobile sur le talus. Un expérimentateur prend place à l’intérieur du chariot et un autre à l’extérieur, lui aussi immobile sur le talus. Un faisceau de lumière est envoyé vers le haut du chariot. Un miroir fixé au plafond retourne le faisceau vers le bas. Un autre miroir fixé sur la table de l’expérimentateur redirige le faisceau vers le plafond. La particule de lumière fait un vas et vient vertical, continuel entre le bas et le haut.
Les deux expérimentateurs voient la situation de façon identique.

Deuxième phase de l’expérience, le chariot se déplace vers la droite à vitesse constante «v». Vu de l’intérieur du chariot, rien ne change, le faisceau continue d’effectuer une trajectoire de vas et vient vertical.
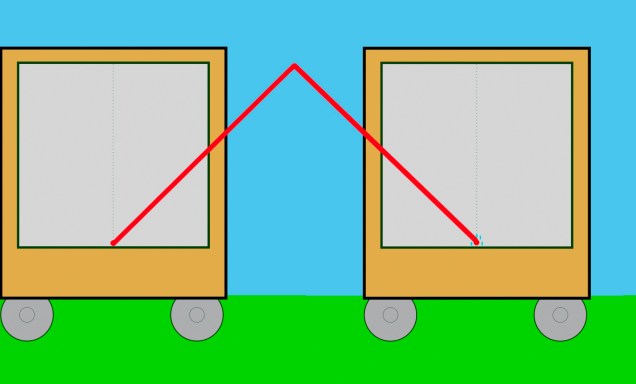
L’expérimentateur sur le talus est toujours immobile et regarde la particule de lumière se déplacer vers la droite. Pour lui, la particule suit une trajectoire triangulaire.
Indépendamment du mouvement du chariot, la particule de lumière se déplace à la même vitesse pour les deux expérimentateurs. Mais vu par l’expérimentateur sur le talus, la particule parcourt un trajet plus long que le trajet vu par l’expérimentateur à l’intérieur du chariot. Voyons cela plus en détail.
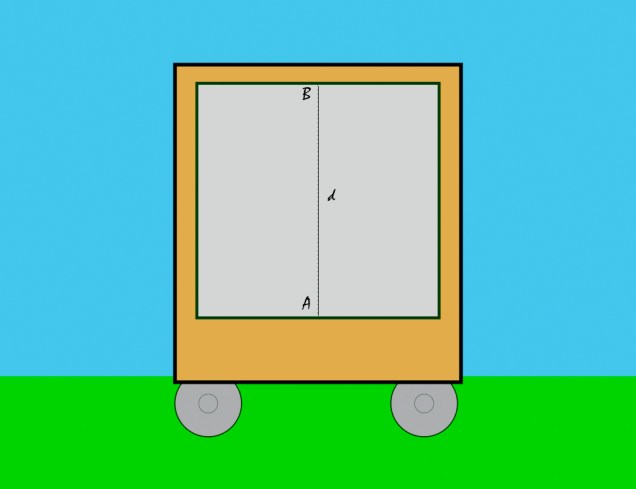
Pour l’expérimentateur à l’intérieur du chariot, la particule de lumière parcourt la distance «d», du point «A» au point «B» à la vitesse de la lumière «c». Le temps de parcours «ti» est donc égal à «d/c» (distance parcourue divisée par la vitesse).
ti = d/c
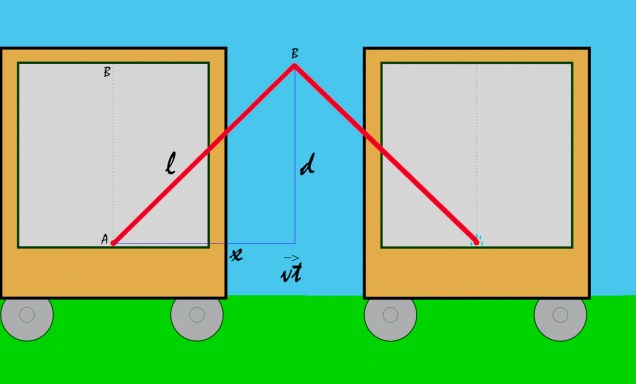
Pour l’expérimentateur à l’extérieur, la particule de lumière parcourt la distance «l», du point «A» au point «B» à la vitesse de la lumière «c». Le temps de parcours «te» est donc égal à «l/c».
te = l/c
Ce qui implique que:
l/c > d/c donc que te > ti
Le temps écoulé pour l’observateur sur le talus est plus grand que le temps écoulé pour l’observateur à l’intérieur du chariot
Le chariot s’est déplacé d’une distance x pendant le temps te à la vitesse v =>

En appliquant le théorème de Pythagore :
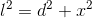
Remplaçons x par v te =>

Isolons d 2 =>

Divisons chacun des côtés par c 2 =>
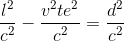
Comme vu plus haut l / c = te et d / c = ti =>



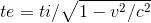
Le temps de ti s’écoule plus lentement que le temps te quand v n’est pas nul. te >= ti.
Comme «c» a une valeur extrêmement plus élevée que les vitesses rencontrées dans la vie courante, l’effet est imperceptible. Cet effet devient important lors de l’étude des particules subatomiques.
Prenons par exemple, une particule subatomique, le muon. Immobile, il a une durée de vie en moyenne de 2,2 microsecondes (immobile ou se déplaçant à très faible vitesse par rapport à c, donc ti = 2,2 microsecondes). Dans l’atmosphère terrestre, où ils sont créés par les rayons cosmiques, ils se déplacent à la vitesse de 298353454 m/s par rapport au sol.
Alors
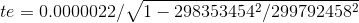
te=2,2E-6/(1-(298353454^2/299792458^2))^(1/2)
te=22,48064 microsecondes
En partant des postulats que la vitesse de la lumière est constante et que les lois de la physique sont identiques dans tout référentiel inertiel, on déduit une dilatation des durées entre deux référentiels en mouvement rectiligne à vitesse constante un par rapport à l’autre. Cette prédiction théorique a été validée à maintes reprises et n’a jamais été prise en défaut.
En physique, on définit « temps propre » τ ( prononcé tau), le temps mesuré par un observateur immobile par rapport au phénomène observé. On dit qu’ils sont dans le même référentiel. C’est le cas pour l’expérimentateur dans le chariot qui est fixe par rapport au jeu de miroirs ou celui dans le laboratoire qui observe un muon immobile ou se déplaçant à faible vitesse par rapport à c. Dans les exemples présentés, ti est le temps propre τ et t le temps du deuxième observateur.
Dilatation du temps
La formule rigoureuse est :
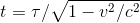
Contraction des longueurs
Maintenant, calculons la distance parcourue par le muon produit dans la haute atmosphère de la terre vue du référentiel terrestre. Sa vitesse par rapport au sol est de 298353454 m/s. Son temps de durée de vie, toujours dans ce même référentiel, est de 22,48064 microsecondes. La distance parcourue est d’ = v t, 298353454 m/s * 22,48064 microsecondes = 6707,2 mètres
d’ = v t = 298353454*22,48064E-6 = 6707,2
Maintenant, calculons la distance parcourue par le muon vue de son propre référentiel. Un observateur «assis» sur le muon observerait un temps de durée de vie de 2,2 microsecondes. Pour lui, la terre s’approche à une vitesse 298353454 m/s. La distance parcourue dans ce référentiel est d = v τ , 298353454 m/s * 2,2 microsecondes = 656,4 mètres.
d = v τ = 298353454*2,2E-6 = 656,4
L’observateur au repos par rapport à la terre mesure 6707,2 m, l’observateur en mouvement par rapport à la terre mesure 656,4 m. Il y a contraction des longueurs dans la direction du mouvement . La particule parcoure le même espace terrestre dans les deux référentiels, mais c’est comme si tout est contracté dans la direction du mouvement incluant l’unité de mesure (la règle en mètre) de l’observateur en mouvement.
Selon la physique classique, le muon créé dans la haute atmosphère devrait franchir que 656 mètres environ, mais dans la réalité nous en retrouvons beaucoup au niveau du sol. La quantité observée correspond aux prédictions de la relativité restreinte.
La formule de la contraction des longueurs
Distance dans le référentiel terrestre : d’ = v t
Distance dans le référentiel de la particule : d = v τ
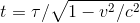
Isolons τ
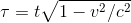
d = v τ
Remplaçons τ

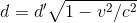
La distance d’ est contractée dans le sens du déplacement. d <= d’.
Dans la vie nous côtoyons couramment l’effet de la contraction des longueurs. Le magnétisme est un effet de cette contraction. Voir les explications sur cette animation.
En partant du fait que la vitesse de la lumière est constante et que les lois de la physique sont identiques dans tout référentiel inertiel, on déduit une contraction des longueurs entre deux référentiels en mouvement rectiligne à vitesse constante un par rapport à l’autre. Cette prédiction théorique a été validée à maintes reprises et n’a jamais été prise en défaut.
La relativité explique ces effets comme conséquences de la structure de l’espace-temps.